I was conversing with blodgett recently on the subject of the large rubber duck I received for Christmas. I found myself unable to give an accurate estimate on how many times larger this new duck was than the regular common rubber duck. I guessed it was perhaps four times as large.
Before reading the rest of the article, you might like to use this image to make your own estimation:
But ill-informed guesswork is not the way of science! A scientist uses the unerring power of logic and experimentation to peer into the darkest corners of human ignorance. To the science laboratory!
Method
An experiment is proposed!
But wait! A good scientist doesn’t dive straight into experimentation without conducting a thorough literature review so that he might know where his contribution fits within the scientific edifice. In this obscure field of measuring how big things are, the most significant work is that of Archimedes who pioneered the “bathtub” technique. We hereby propose to extend this technique to the measuring of rubber ducks.
Background research now completed, we proceed to define our experimental method. The size of the duck shall be defined by the volume of water it displaces. An alternative method whereby the duck is filled with water via its valve, was discounted due to considerations for duck welfare and unequal rubber thickness. However, the duck-valve cannot be ignored as it may admit water during the experiment: to ameliorate this we cover the valve with sellotape.
The steps are as follow:
- A jug is filled with 300ml of water.
- The duck is placed in the water such that the water covers the duck’s head. Special care must be taken that fingers or other implements do not affect the result.
- The combined volume of duck and water is read off and 300ml is subtracted, yielding the volume of the duck.
- The jug is refilled to 300ml and the experiment repeated.
Here is a diagram of the experimental apparatus:
Results
First, we perform the experiment on the large duck:
The measurement is 450ml, giving a duck volume of 150ml.
Next, we repeat the experiment with the small duck:
The measurement is 350ml, which means the small duck has a volume of 50ml.
The experiment completed, we tidy the laboratory and proceed to an in-depth analysis of the results.
Analysis
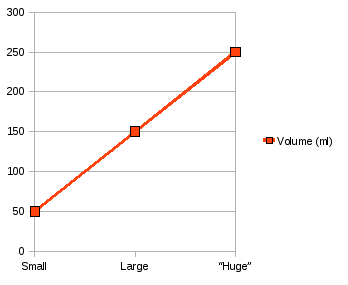
A simple numerical analysis reveals that the large duck is 150.0 / 50.0 = 3.0 times larger than the small duck. This means my original prediction had an error of 25%.
The significance of this outcome can be better appreciated with a bar chart:
What predictions does this result allow us to make? Well, it can be easily seen that there is a linear relationship between duck size and volume. We see no reason why this cannot be extrapolated to hypothesise the existence of a new class of “huge” rubber duck which might have a volume of 250ml!
Alarmingly, this data also predicts that a hypothetical “tiny” class of rubber duck would have negative volume! Such a troubling thought is best not dwelled upon, especially as it’s time for lunch.










 Posts
Posts
since size cannot be negative, maybe it’s a power law rather than a linear one? i think this will result in tiny being very small.
January 3, 2010 @ 6:16 pm
I LIKE IT!!
:D :D
January 3, 2010 @ 6:32 pm
and it is indeed very tall duck
January 3, 2010 @ 6:32 pm
> and it is indeed very tall duck
Ja, it’s quite tall relative to the small duck. Can’t find a ruler to measure it unfortunately :-(
January 6, 2010 @ 7:38 am
> since size cannot be negative, maybe it’s a power law rather than a linear one?
Let’s assume this forms the “further work” section.
January 6, 2010 @ 7:39 am